Inhaltsverzeichnis
1. Reflektion am ebenen Spiegel
2. Wahl eines kreisförmigen Hohlspiegels
3. Kennzeichnungen am Hohlspiegel
4. Reflektion von Strahlen parallel zur optischen Achse
5. Abbildungen am Hohlspiegel
6.
7. Abbildungsgesetz am Hohlspiegel (Excel-Tabelle)
8. Abbildungen am Hohlspiegel
Wenn ein Lichtstrahl nicht senkrecht auf einen ebenen Spiegel trifft, wird der Lichtstrahl auf einem ganz bestimmten Winkel zurückgeworfen. Es gilt das Reflexionsgesetz am Planspiegel. (Planspiegelgesetze- Gegenüberstellung)
2. Wahl eines kreisförmigen Hohlspiegels
Man kann nun versuchen herauszufinden, welchen Weg der reflektierte Lichtstrahl an gekrümmten Flächen nimmt. Dazu wählt man als Einstieg eine einfache regelmäßig gekrümmte Fläche. Einfach kann heißen, leicht herstellbar oder leicht zu verstehen.
Hier wird ein kreisförmiger Hohlspiegel gewählt. (Definitionen am Kreis, Definitionen für kreisförmige Hohlspiegel)
3. Kenzeichnungen eines Hohlspiegels
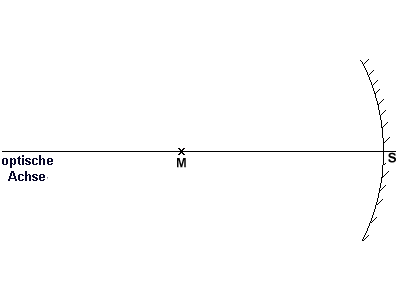
Der Hohlspiegel wird mit einer Schraffur als undurchsichtiger Körper gekennzeichnet. Die räumliche Mitte des Holspiegels bezeichnet man als Scheitel S. Vom Scheitel durch den Mittelpunkt M verläuft eine Gerade, die man optische Achse nennt.
4. Reflektion eines Strahls parallel zur optischen Achse
Zunächst stellt man einen Gegenstand vor den kreisförmigen Hohlspiegel in etwa dem Abstand des (geschätzten) Durchmessers.
Von der Spitze des Gegenstandes soll ein beliebiger Strahl den Hohlspiegel im Punkt A treffen. Da ein Strahl unendlich dünn ist, ist die Fläche, auf der er im Punkt A auftrifft, praktisch als ebene Fläche anzusehen. Man kann sich daher den Hohlspiegel an dieser Stelle durch ein kleines Planspiegelchen ersetzt denken, der den gleichen Winkel zum einfallenden Strahl besitzt wie der Hohlspiegel.
Will man den kleinen Planspiegel im richtigen Winkel zeichnen, so kann man gut die Geometrie am Kreis benutzen:
Verbindet man den Auftreffpunkt des Lichtstrahls mit dem Mittelpunkt des Kreises, so erhält man den Radius im Auftreffpunkt. Der Radius steht immer senkrecht auf der Kreislinie (Peripherie). Deshalb ist die Senkrechte auf dem Radius im Auftreffpunkt die Tangente an den Kreis in diesem Punkt und stellt gleichzeitig die Oberfläche des gedachten Planspiegelchen dar.
Daher ist der Winkel zwischen dem Radius und dem einfallenden Strahl der Einfallswinkel. Für den kleinen gedachten Planspiegel an der Stelle A gilt deshalb das schon bekannte Reflektionsgesetz am Planspiegel. Somit erhält man den Weg des reflektierten Strahls.
Führt man die gleiche Konstruktion mit anderen Strahlen, die parallel zur optischen Achse und nahe daran sind, durch, so stellt man fest, dass alle reflektierten Strahlen sich in einem Punkt treffen. Diesen Punkt nennt man Brennpunkt F (lat. focus der Herd)
5. Abbildungen am Hohlspiegel
Zunächst stellt man einen Gegenstand vor den kreisförmigen Hohlspiegel in etwa dem Abstand des (geschätzten) Durchmessers.
Von der Spitze des Gegenstandes soll ein beliebiger Strahl den Hohlspiegel im Punkt A treffen. Da ein Strahl unendlich dünn ist, ist die Fläche, auf der er im Punkt A auftrifft, praktisch als ebene Fläche anzusehen. Man kann sich daher den Hohlspiegel an dieser Stelle durch ein kleines Planspiegelchen ersetzt denken, der den gleichen Winkel zum einfallenden Strahl besitzt wie der Hohlspiegel.
Will man den kleinen Planspiegel im richtigen Winkel zeichnen, so kann man gut die Geometrie am Kreis benutzen:
Verbindet man den Auftreffpunkt des Lichtstrahls mit dem Mittelpunkt des Kreises, so erhält man den Radius im Auftreffpunkt. Der Radius steht immer senkrecht auf der Kreislinie (Peripherie). Deshalb ist die Senkrechte auf dem Radius im Auftreffpunkt die Tangente an den Kreis in diesem Punkt und stellt gleichzeitig die Oberfläche des gedachten Planspiegelchen dar.
Daher ist der Winkel zwischen dem Radius und dem einfallenden Strahl der Einfallswinkel. Für den kleinen gedachten Planspiegel an der Stelle A gilt deshalb das schon bekannte Reflektionsgesetz am Planspiegel. Somit erhält man den Weg des reflektierten Strahls.
Führt man die gleiche Konstruktion mit anderen Strahlen, die parallel zur optischen Achse und nahe daran sind, durch, so stellt man fest, dass alle reflektierten Strahlen sich in einem Punkt treffen. Diesen Punkt nennt man Brennpunkt F (lat. focus der Herd)
Weitere Links
Literatur