Inhaltsverzeichnis
1. Bildliche Darstellung des Kreises
2. Bezeichnungen am Kreis
3. Bildliche Darstellung von Geraden und Kreis
4. Bezeichnungen von Geraden am Kreis
5. Bildliche Darstellung von Winkeln am Kreis
6. Bezeichnung von Winkeln am Kreis
7. Sätze für Tangente und Radius
2. Kreisbezeichnungen
Eine Kurve, die von einem Punkt aus immer den gleichen Abstand besitzt, nennt man
einen Kreis 
.
Die äußere Umschließung eines Kreise heißt Kreislinie, Peripherie oder Umfang
U .
Der Kreis bedeckt in einer Ebene eine Kreisfläche F ..
Der Punkt, von dem die Kreislinie den gleichen Abstand besitzt, nennt man (Krümmungs-)
Mittelpunkt
M des Kreises
(s.a. Gerade und Kreis).
Die Strecke mit den Endpunkten auf dem Umfang heißt
Sehne s
(s.a. Gerade und Kreis).
Die Sehne, die durch den Mittelpunkt eines Kreises geht, heißt Durchmesser
d .
Die Verbindungslinie vom Mittelpunkt mit der Peripherie heißt Radius
r .
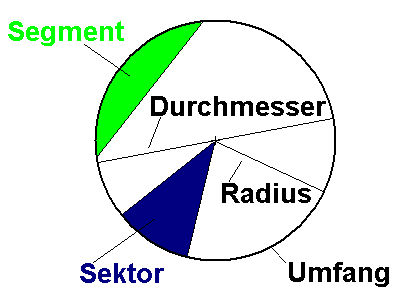
Die Fläche, die durch eine Sehne von einem Kreis abgeschnitten wird, nennt man Segment.
Die Fläche zwischen zwei Radien heißt Sektor
.
Bezeichnungen am Kreis
3. Bildliche Darstellung von Geraden und Kreis
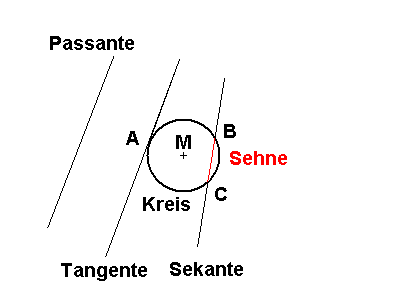
Bildliche Darstellung von Geraden und Kreis
4. Bezeichnungen von Geraden am Kreis
Verläuft eine Gerade an einem Kreis vorbei, ohne den Kreis zu berühren, so nennt man die Gerade in Bezug zum Kreis eine Passante.
Berührt die Gerade die Kreislinie in genau einem Punkt, so nennt man die Gerade eine Tangente,
den Punkt nennt man Berührungspunkt (im Bild A) .
Schneidet die Gerade die Kreislinie in zwei Punkten, so spricht man von einer Sekante
.
Das Teilstück der Sekante, das innerhalb des Kreise verläuft, heißt Sehne
mit den Endpunkten B und C ,
die beiden Teilstücke des Kreise, die durch die Sehne getrennt sind,
heißen Bogen.
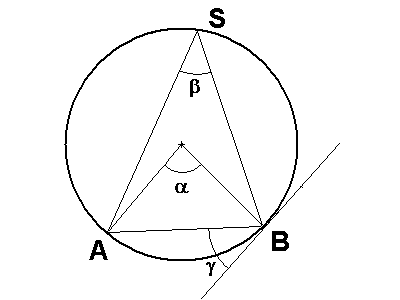
5. Winkel am Kreis
Gegeben ist ein Kreis mit einer Sehne AB und einer Tangente an den Kreis mit dem Berührungspunkt B. Der Punkt S auf der Umfangslinie (Peripherie) ist mit den beiden Endpunkten der Sehne A und B verbunden.
Definitionen:
Der Winkel alpha wird gebildet aus den Beiden Radien zu den Endpunkten der Sehen A und
B und heißt Mittelpunktswinkel (Zentriwinkel)
.
Der Winkel beta wird gebildet aus den Verbindungslinien des Punktes S mit dem beiden
Endpunkten der Sehne A und B und heißt Umfangswinkel (Peripheriewinkel)
.
Der Winkel gamma wird gebildet aus der Tangente im Punkte B mit der Sehne AB und hat
den Namen Sehnentangentenwinkel
.
Es gelten die Sätze:
- Alle möglichen Peripheriewinkel sind untereinander gleich groß.
- Der Peripheriewinkel ist halb so groß wie der Zentriwinkel über dem gleichen Bogen.
- Der Sehnentangentenwinkel und der Peripheriewinkel sind gleich groß.
- Alle Radien sind gleich lang.
- Der Radius steht immer senkrecht auf der Kreislinie.
- Die Senkrechte zum Radius im Berührungspunkt ist die Tangente an den Kreis.
haeusler[at]muenster[dot]de Kurve
Weitere Links
Literatur